Evaluating shooting skills of soccer players: a Bayesian model averaging approach
Vienna University of Economics and Business
Jan 17, 2025
Introduction
Motivation
How can evaluate the shooting skills of a soccer player?
Count how many goals a player scored during a season.
- Problem: Scoring highly depends on the circumstances of each shot.
- Solution: xG models \(\Rightarrow\) model success probability dependent on various important factors.
Count xG generated from shots and compare to actual goals (in a season).
- Problem: No stability, no uncertainty quantification.
Idea: Test whether player significantly impacts outcome of a shot.
Data
Event Stream Data:
- All shots (and other actions) from 5 Big European leagues from 2015/16 season
- 45198 shots (4308 resulted in goals, i.e. ~10%)
Features for each shot:
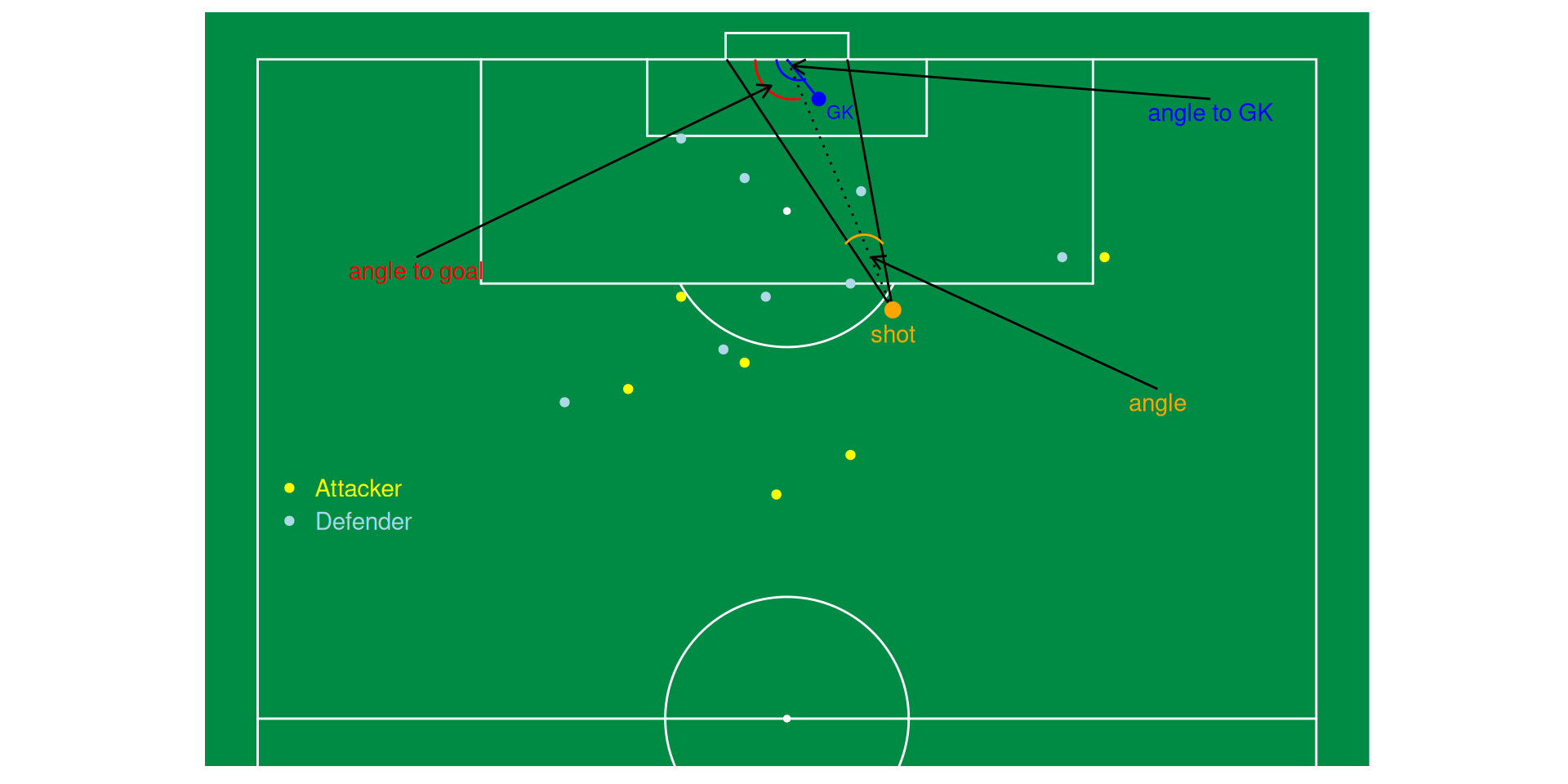
- 20 Explanatory variables (shot distance, shot angle, distances to defenders and goalkeepers,…)
- Outcome variable (shot result: goal/no goal)
- For each shot: shooter is known (~ 1000 distinct players took a shot in our data).
Data
Methodology
Methodology
Goal: Infer effect of a specific player on the outcome of a shot
Use Bayesian model averaging to infer player effects.
Challenge 1: Huge number of players.
- Which players have a measurable effect on the outcome of a shot? Which players should be included in a shot model?
- Computational expense of large number of variables?
Challenge 2: Binary outcome of the data.
BMA for logistic regression?
Binary outcome \(\Rightarrow\) Use Bayesian modelling averaging for logistic regression!
Approach 1: Use package
BMA(Raftery et al. 2024) and functionbic.glm.- Problem: Code is still running (since last wednesday).
Ok, so lets reduce the number of players and look for another solution.
- Only consider forwards and strikers (265 player instead of 1067).
Approach 2: Use package
BAS(Clyde 2024) and functionbas.glm.- Code ran 2 days (🎉 we’re getting better 🎉)
- Problem: still a long time \(\rightarrow\) tuning of default setup.
- Approach 3: Use linear probability model.
Linear Probability Model
Simply fit a linear model to binary outcome data \(\Rightarrow\) package BMS (Feldkircher and Zeugner 2015) for BMA.
Start with moderate default parameters and smaller dataset (reduced number of players):
- Runtime: ~3 Sec 🎆 🎇 🎆.
- Disadvantages:
- Deliberate misspecification: possibility of getting probabilities above (below) 1 (0).
- Advantages:
- Runtime: possibility to explore different setups.
- Interpretation is still possible.
- No issue with non-collapsibility.
Results
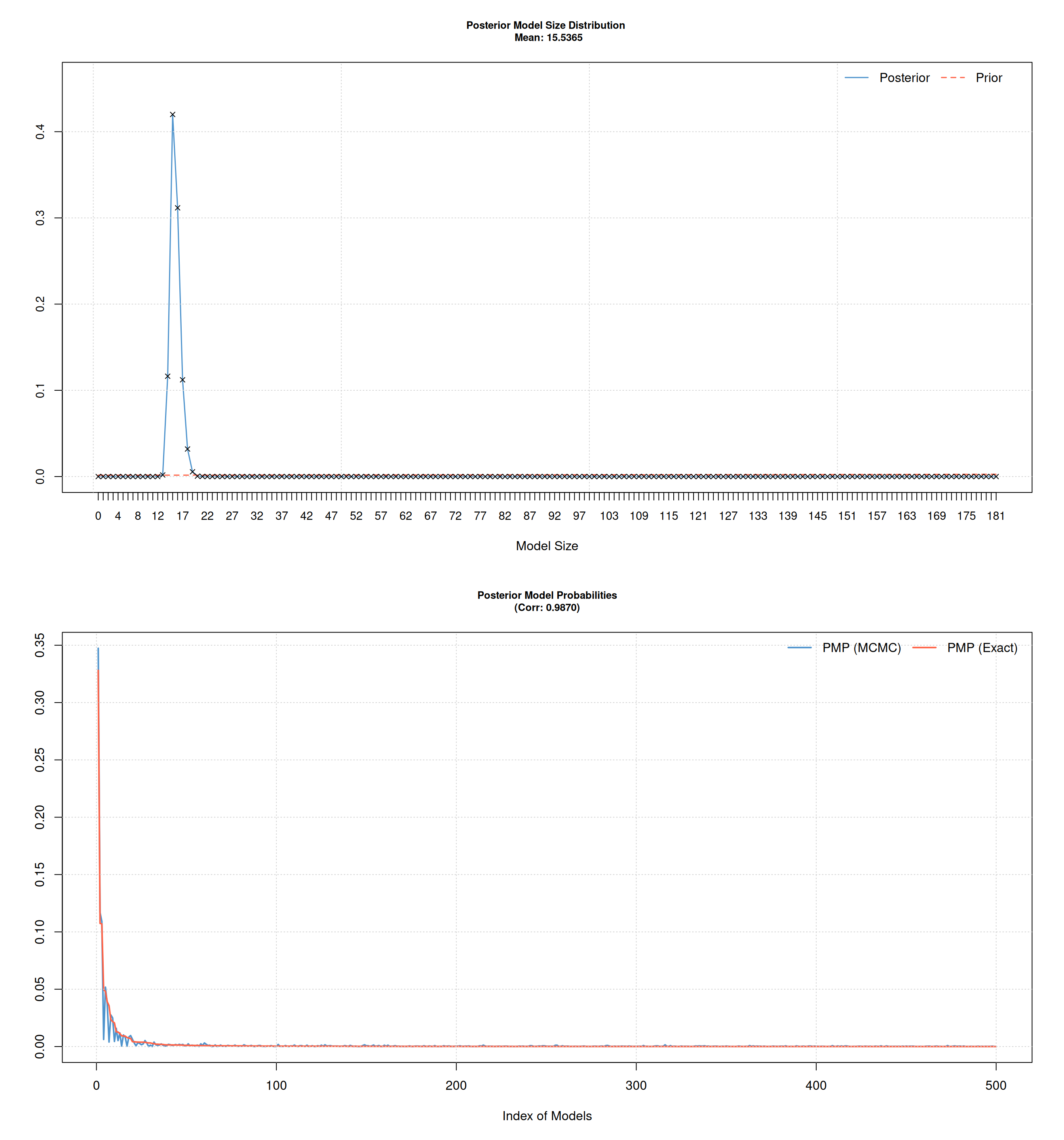
First results
Fix shot specific variables \(\Rightarrow\) always included:
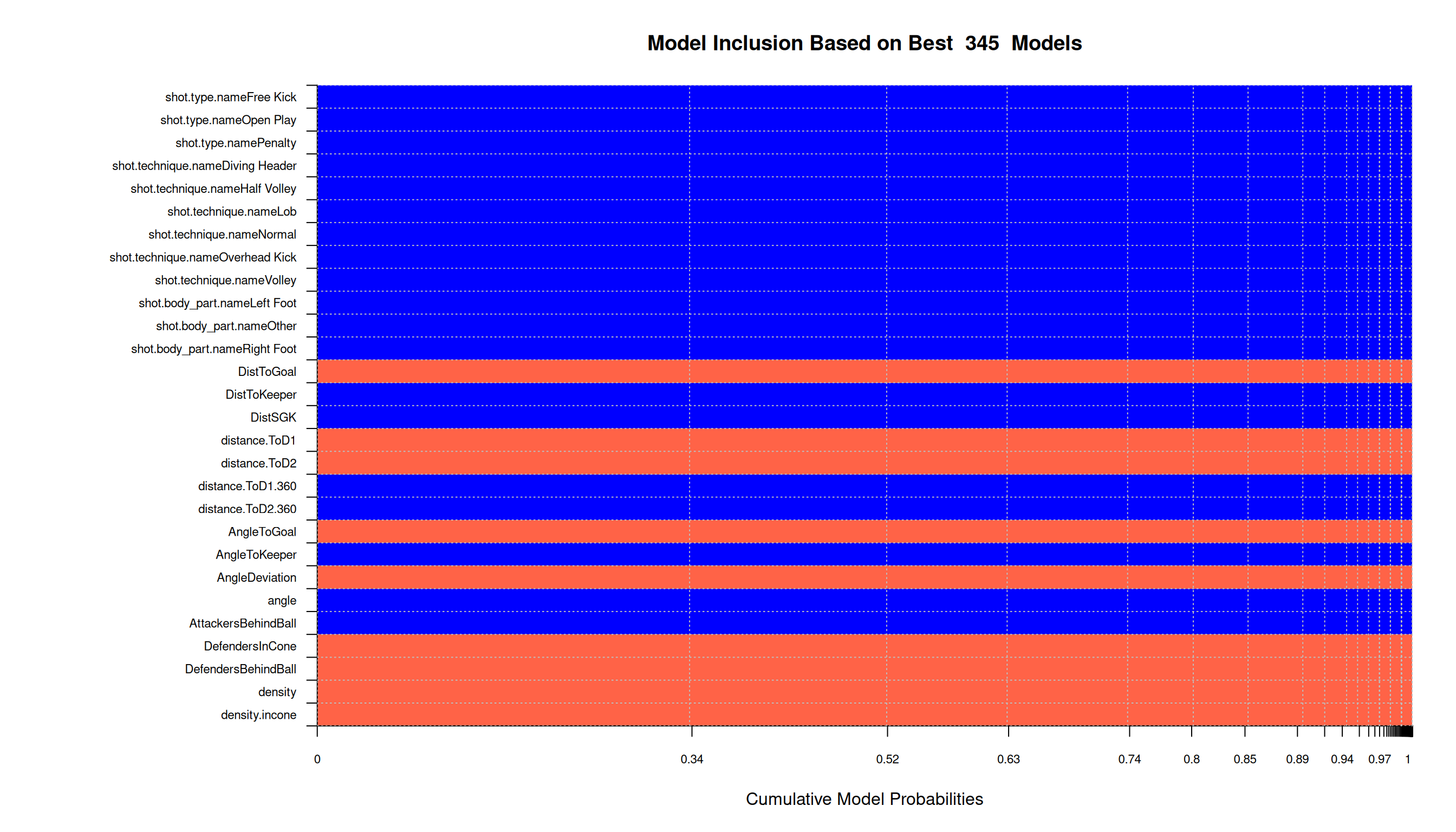
First results
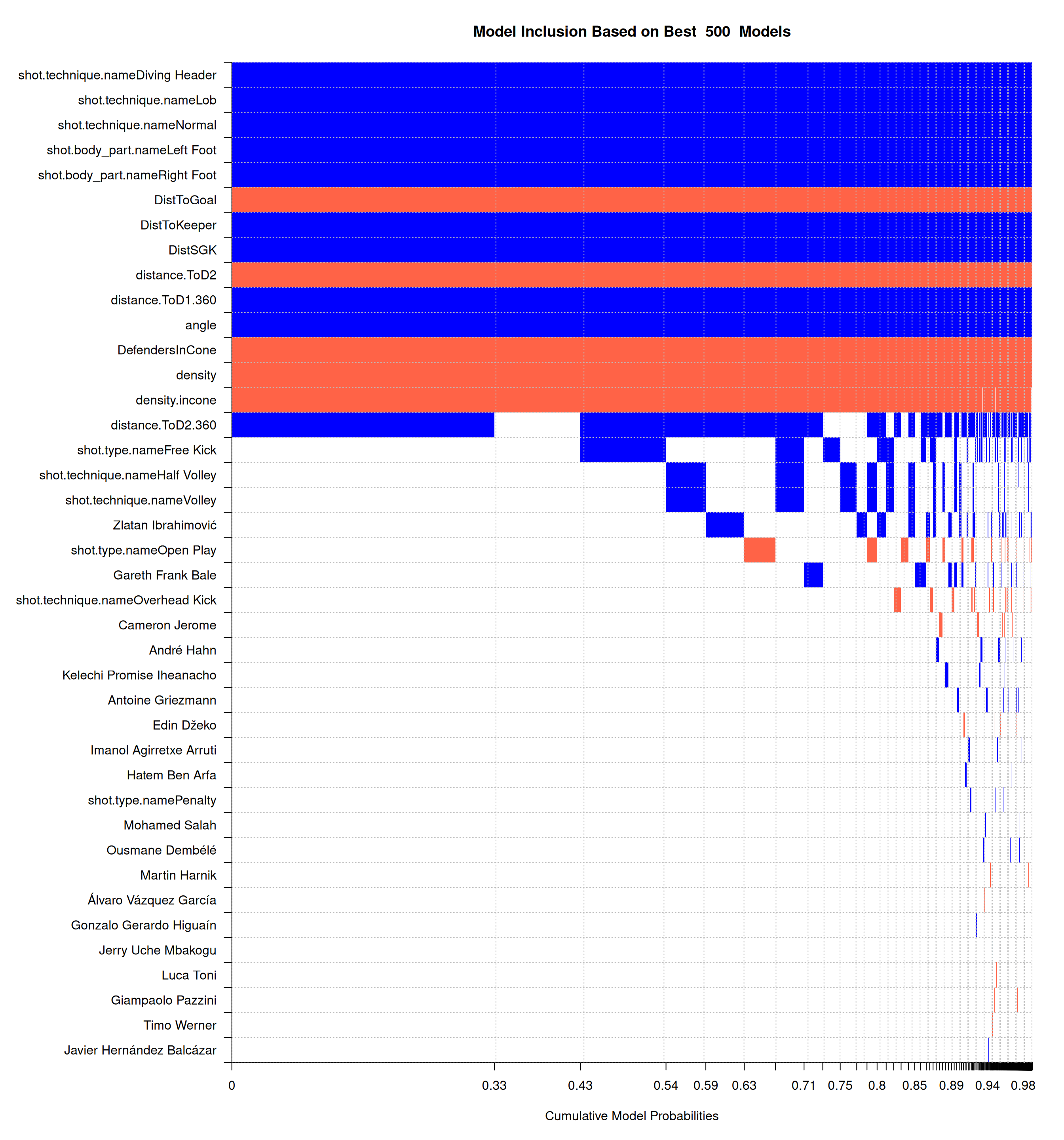
We are interested in player evaluation \(\Rightarrow\) top 20 w.r.t inclusion:
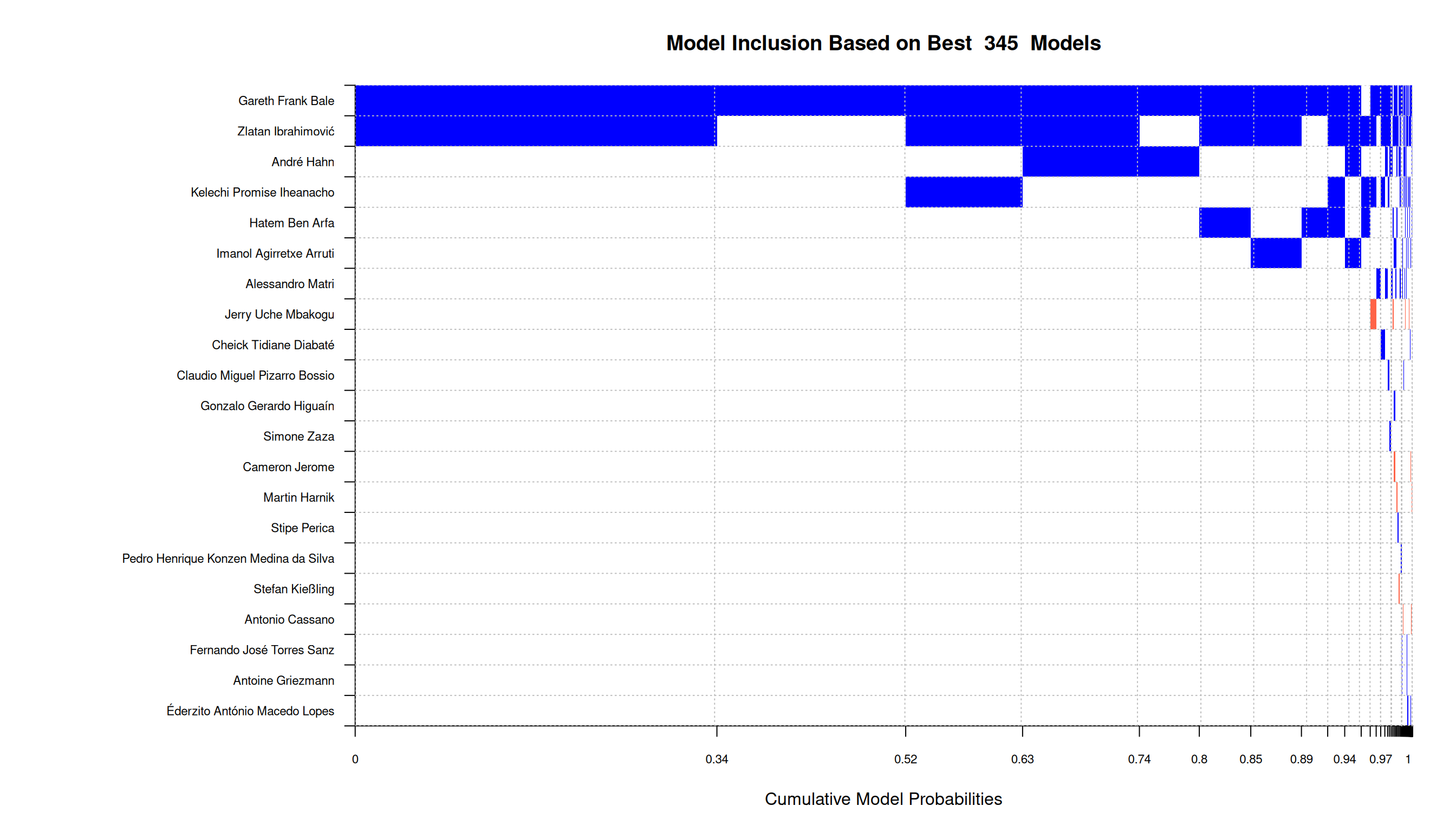
Model?
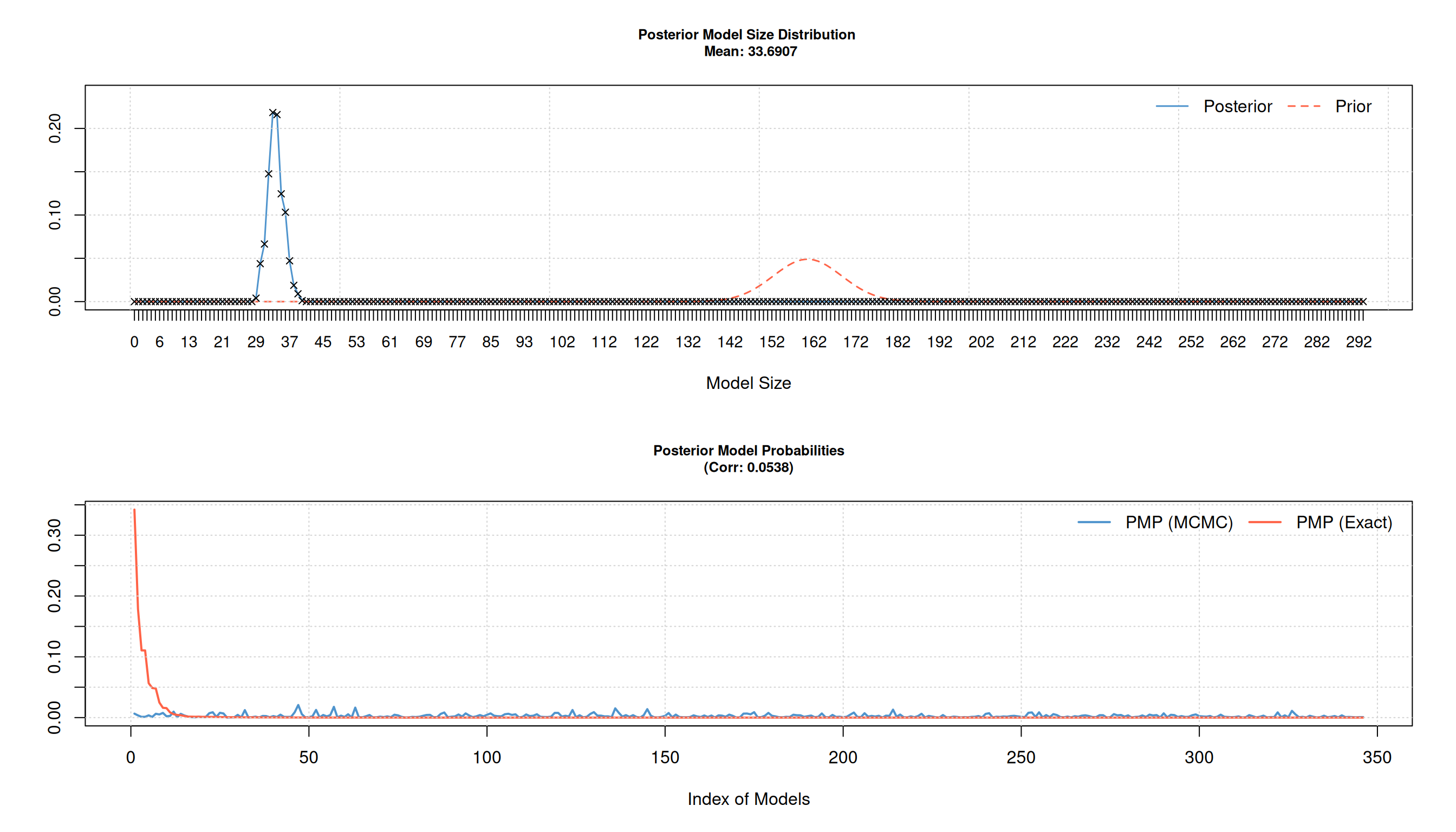
Second Results
Adjust prior based on previous observations:
Recap of results
First results:
- Fix shot specific variables \(\Rightarrow\) interested in player \(\beta\)’s adjusted for shot circumstance.
- Default setup and fixed prior on model size (\(p/2\)).
- after 10000 iteration \(\Rightarrow\) no convergence of sampler (Correlation of PMP (MCMC) and PMP(Exact) very low).
- posterior model size distribution suggest smaller models with barely players selected.
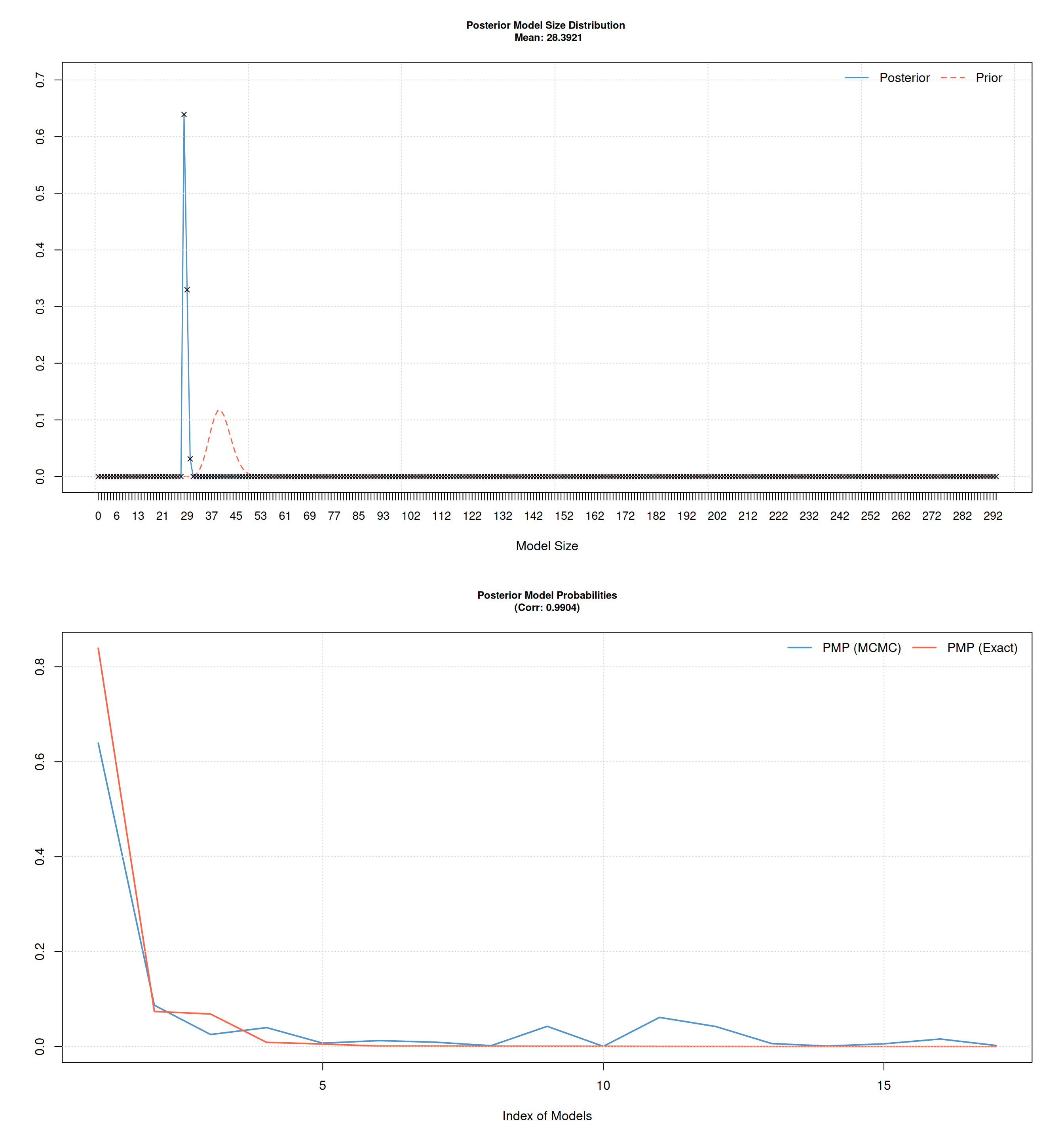
Second results:
- A priori smaller model size.
- High PMP correlation after low number of iteration (10000).
- Only small amount of players selected (small PIP) \(\color{red}{\Rightarrow}\) goal is evaluating players!
A model for player evaluation
Recall: Goal is to evaluate shooting skills of players.
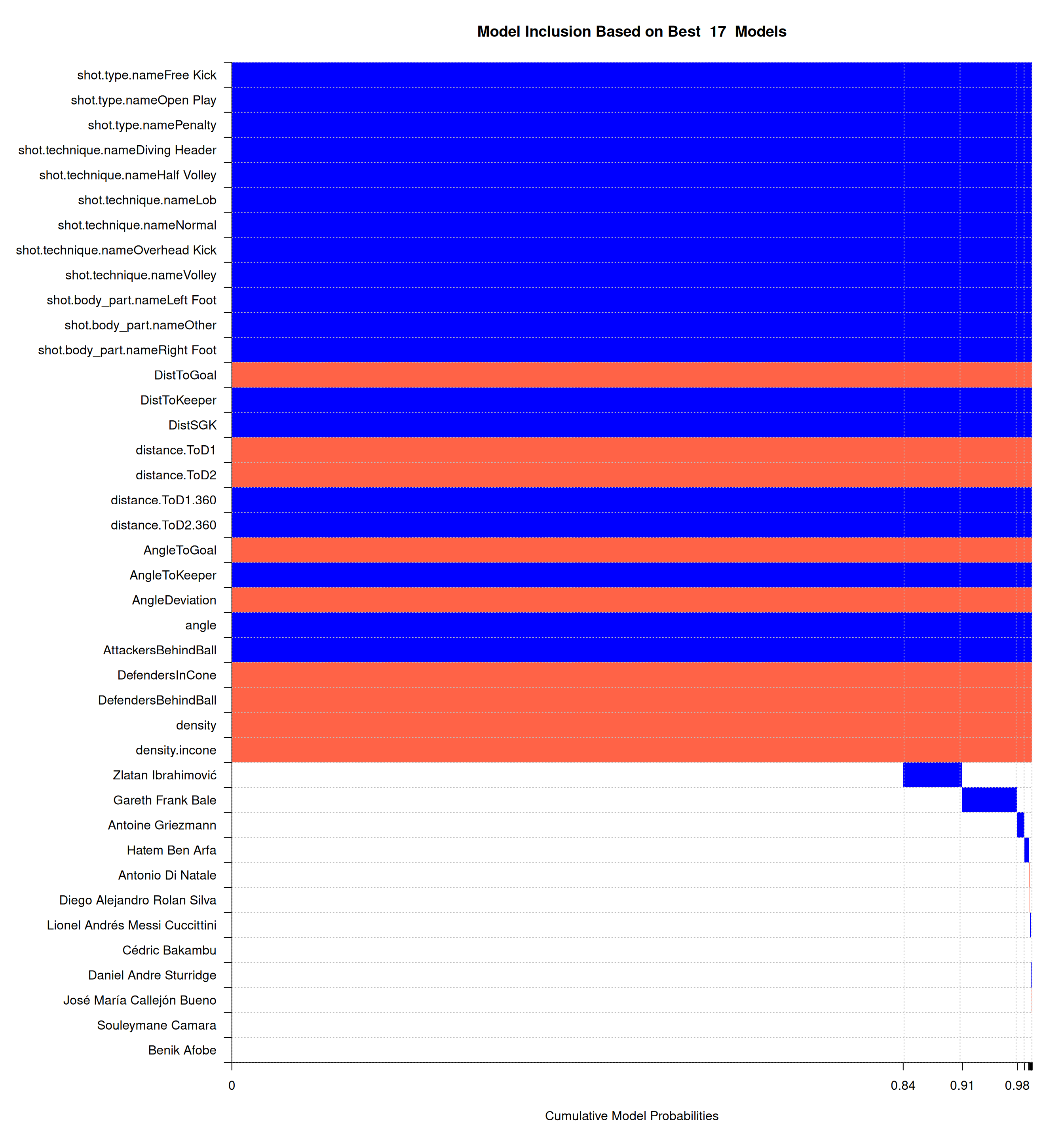
Set prior model size parameter purposely high (~ 200 variables).
Increase MCMC iterations:
- Burn-in: 200000 steps.
- Iterations: 5000000.
- Retain 5000 best model.
- Still feasible with
BMS: Runtime ~5 min.
Model
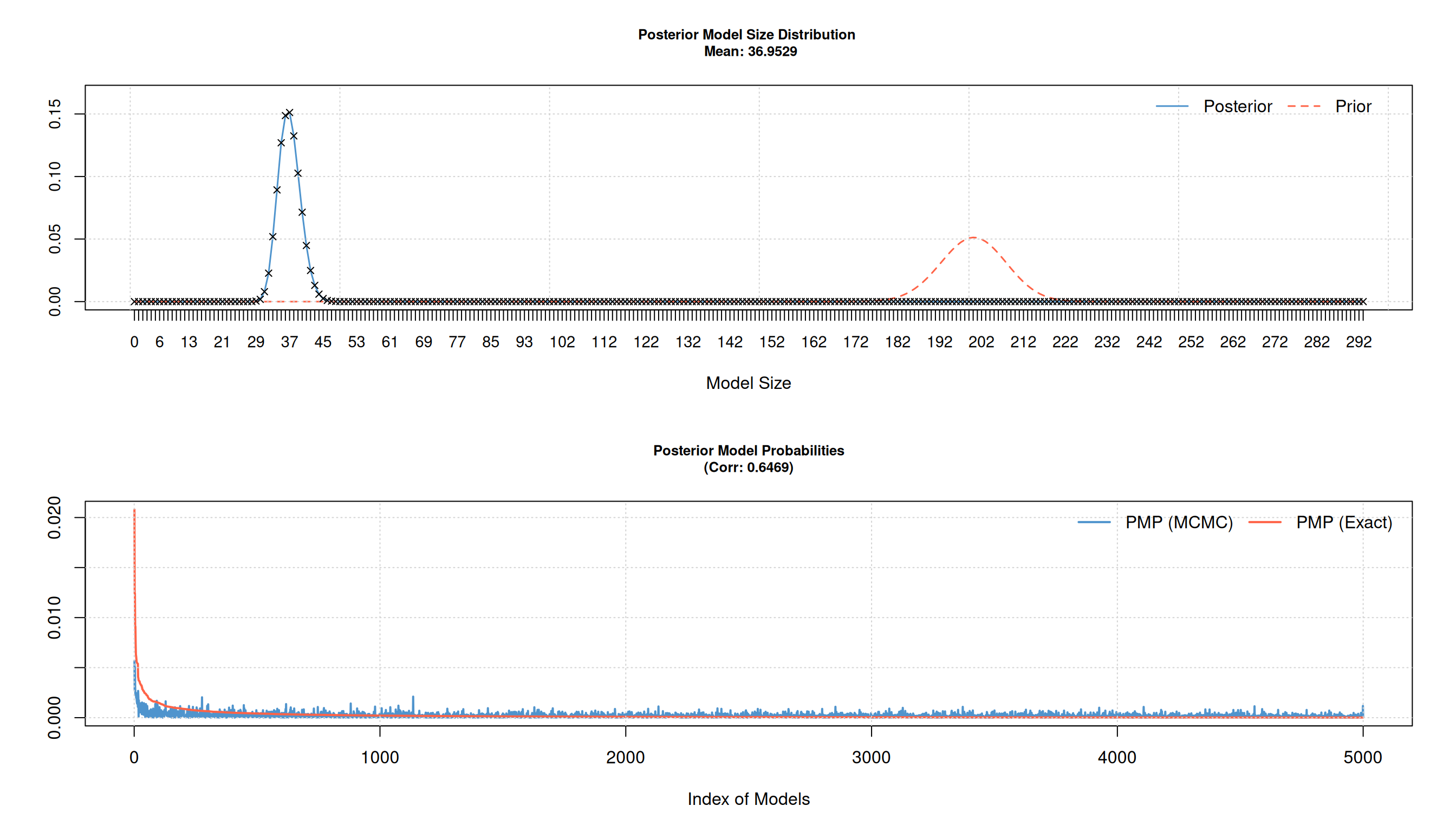
Top 20 players PIP
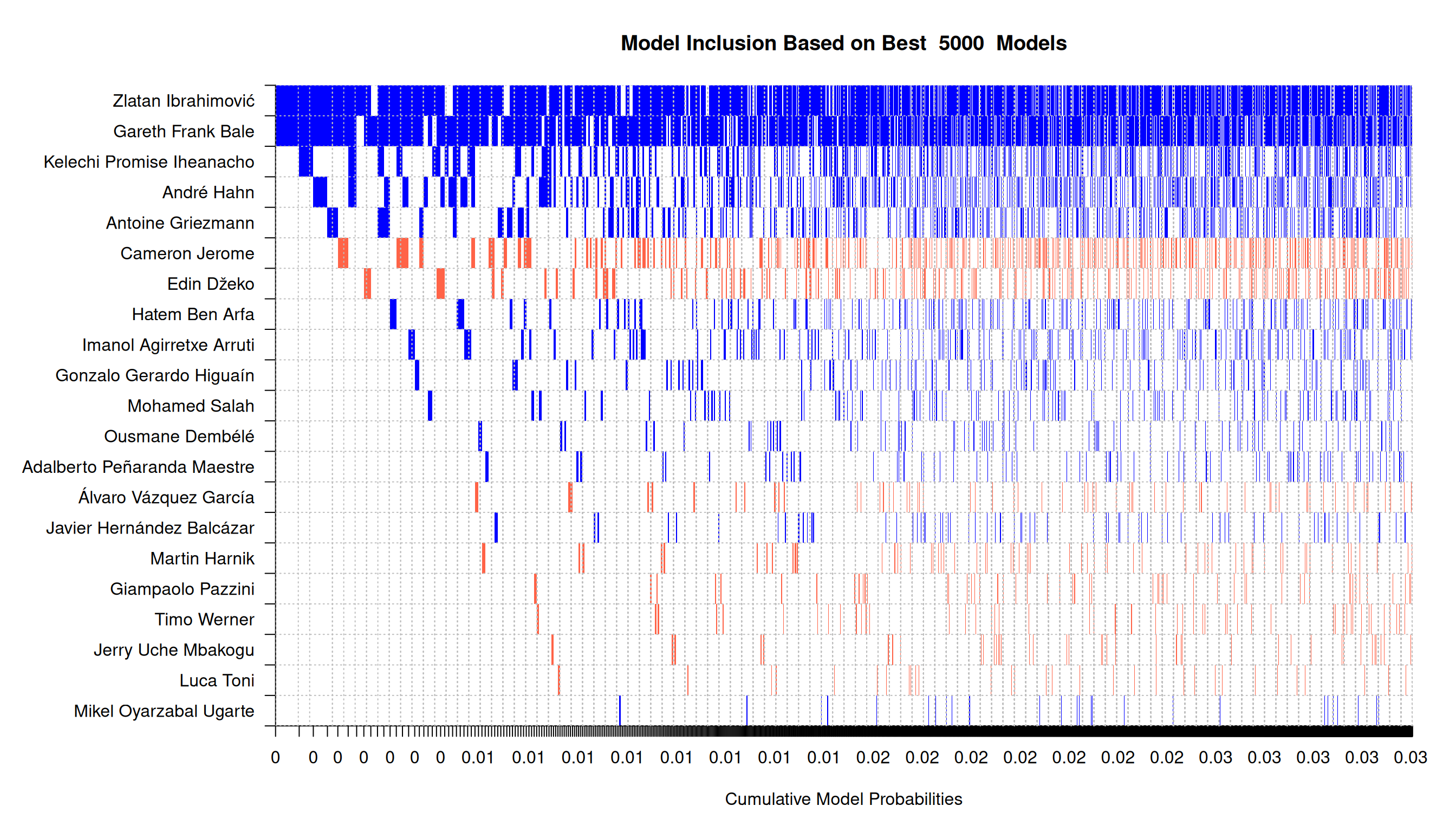
Top 20 players beta
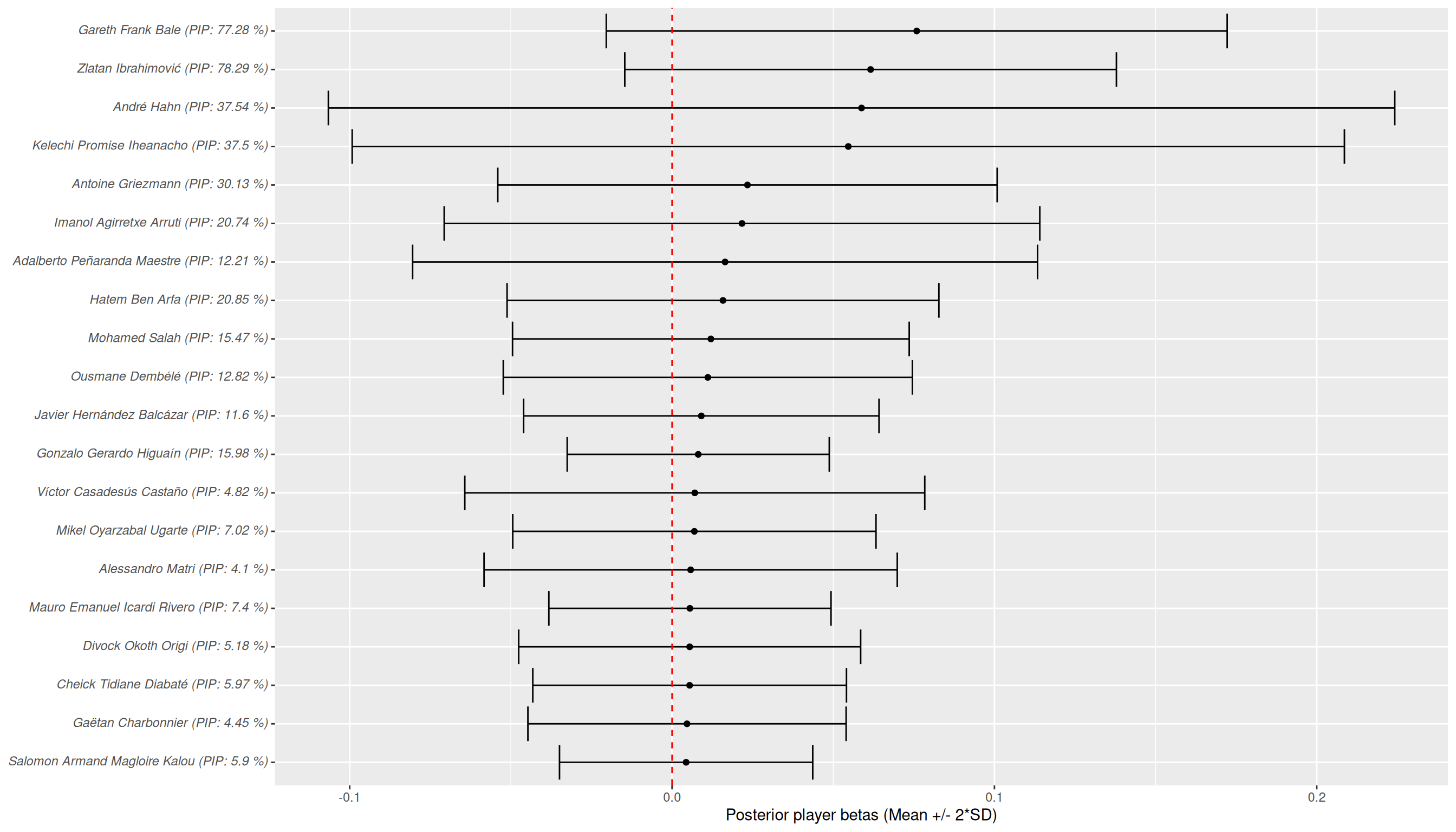
Messi vs Ronaldo
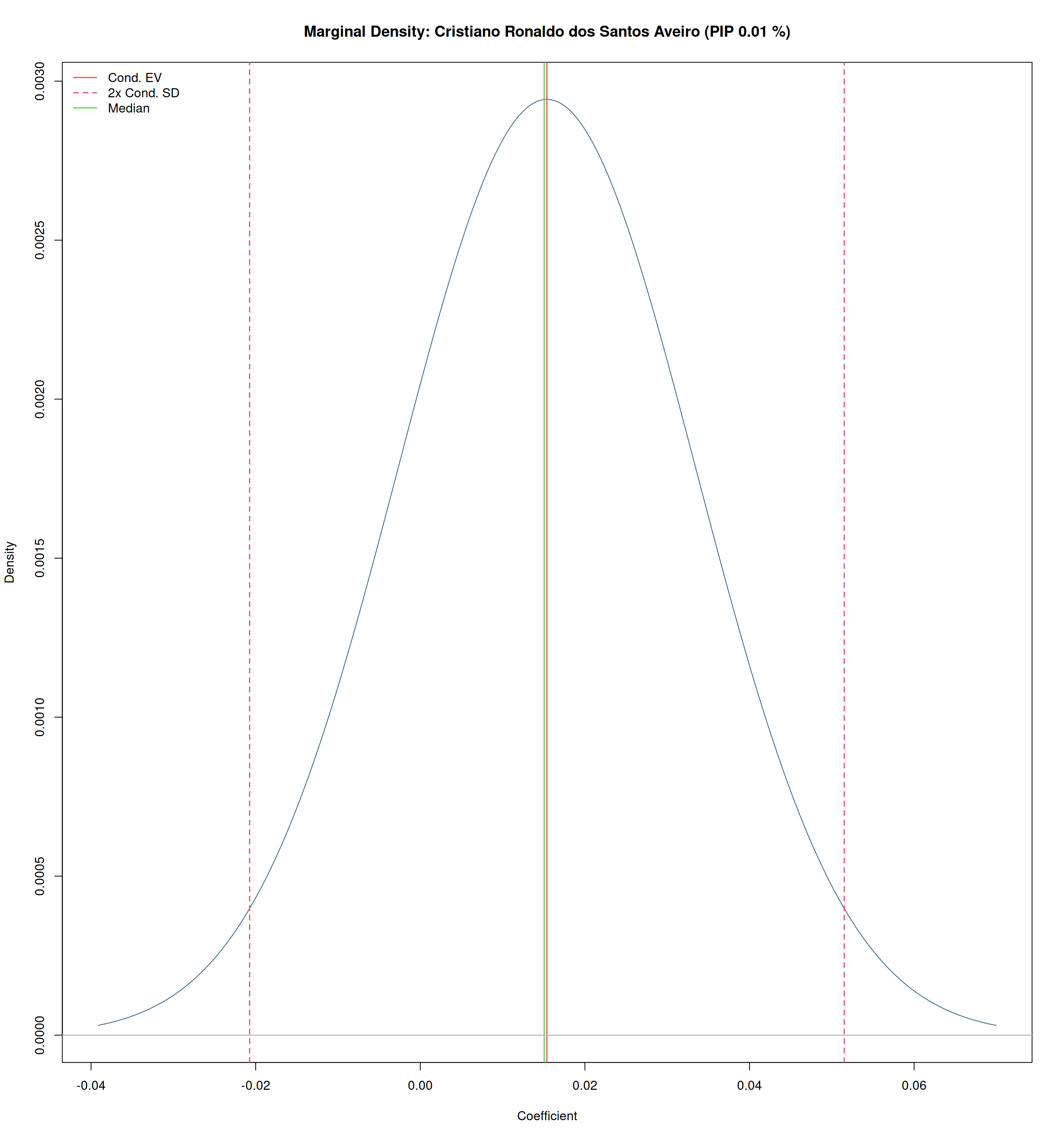
Summary
Goal: Use BMA to evaluate shooting skill of players.
Preliminary findings:
- Zlatan is the best…

Summary
Goal: Use BMA to evaluate shooting skill of players.
Preliminary findings:
Zlatan is the best…
… or maybe Bale??
Summary
Goal: Use BMA to evaluate shooting skill of players.
Preliminary findings:
- Analyzing shooting skills is difficult (at least with the data at hand).
- Circumstances of shots are more important than shooters.
Summary
Goal: Use BMA to evaluate shooting skill of players.
Preliminary findings:
- Analyzing shooting skills is difficult (at least with the data at hand).
- Circumstances of shots are more important than shooters.
Further results (Appendix):
- Do not fix shot specific variables.
- Vary prior setups for betas and model size.
- Combination of models.
Summary
Goal: Use BMA to evaluate shooting skill of players.
Preliminary findings:
- Analyzing shooting skills is difficult (at least with the data at hand).
- Circumstances of shots are more important than shooters.
Further results (Appendix):
- Do not fix shot specific variables.
- Vary prior setups for betas and model size.
- Combination of models.
Outlook and Discussion:
- LPM vs. logistic regression.
- Include all players.
- xG literature (and results) suggest non-linear relationships between shot specific variables.
- Model agnostic tests.
References
Appendix
Further results I
Do not fix shot specific variables, but keep prior fixed at large models:
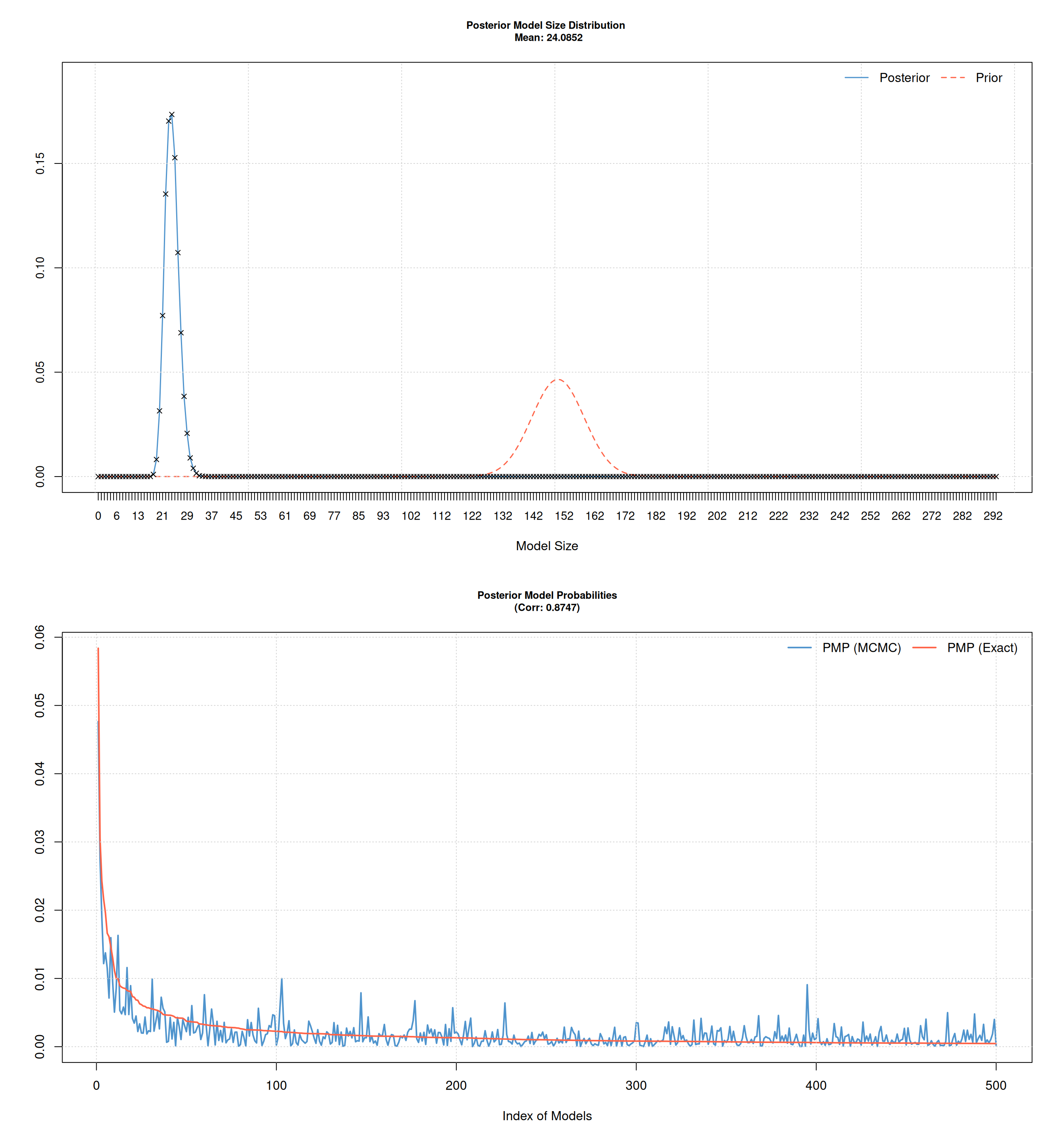
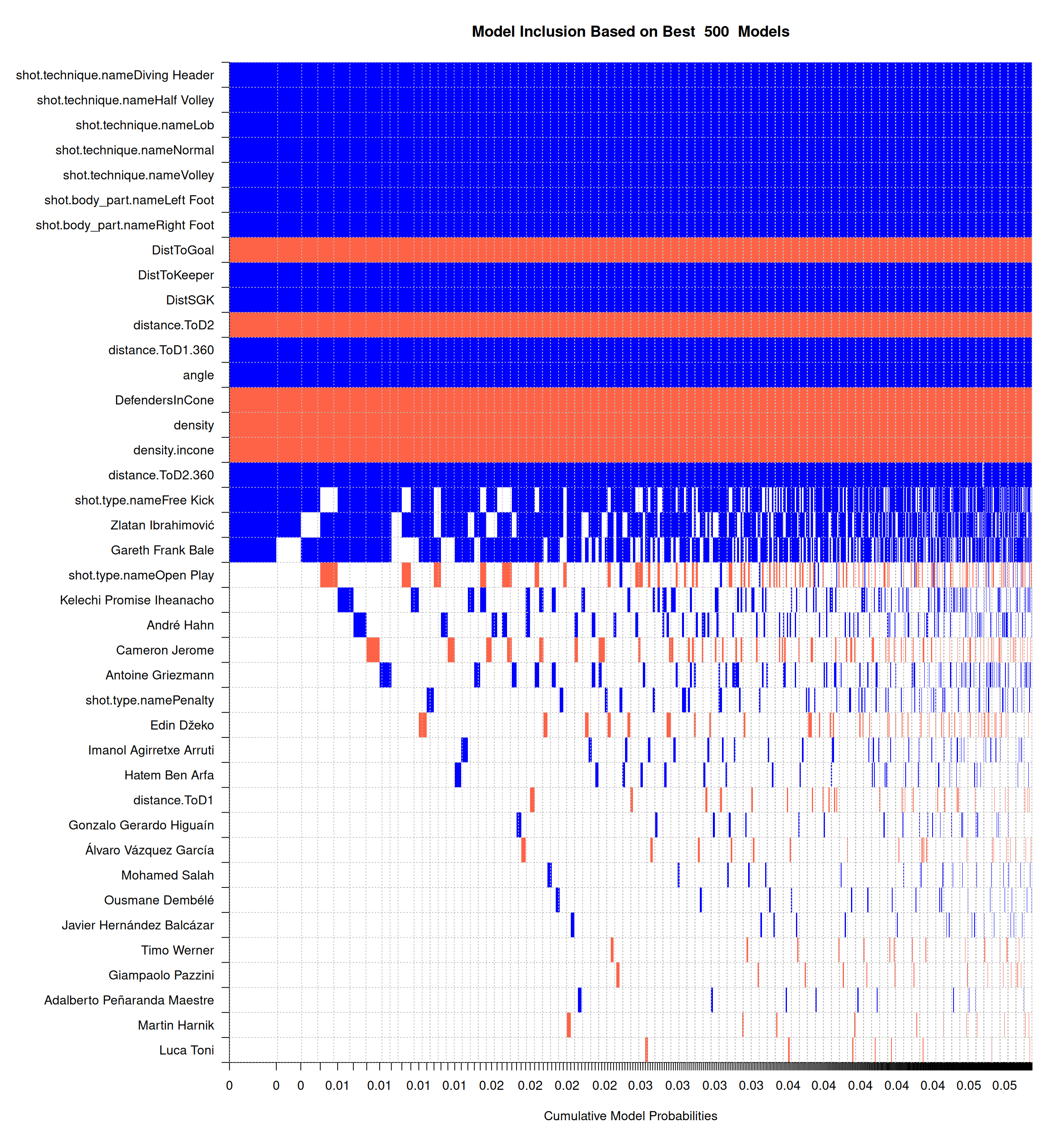
Further results II
Hyperprior on model size, BRIC on \(g\).