Bayesian model averaging for logistic regression: Evaluating shooting skills of soccer players

Robert Bajons and David Hirnschall

Vienna University of Economics and Business

Nov 22, 2024

Motivation

How can evaluate the shooting skills of a soccer player?

  • Count how many goals a player scored during a season.

    • Problem: Scoring highly depends on the circumstances of each shot.
    • Solution: xG models \(\Rightarrow\) model success probability dependent on various important factor.

  • Count xG generated from shots and compare to actual goals (in a season).

    • Problem: No stability, no uncertainty quantification.

  • Idea: Test whether player significantly impacts outcome of a shot.

Data

  • Event Stream Data:

    • All shots (and other actions) from 5 Big European leagues from 2015/16 season
    • 45198 shots (4308 resulted in goals, i.e. ~10%)

  • Features for each shot:

    • 21 Explanatory variables (shot distance, shot angle, distances to defenders and goalkeepers,…)
    • Outcome variable (shot result: goal/no goal)
    • For each shot: shooter is known (~ 1000 distinct players took a shot in our data).

Data

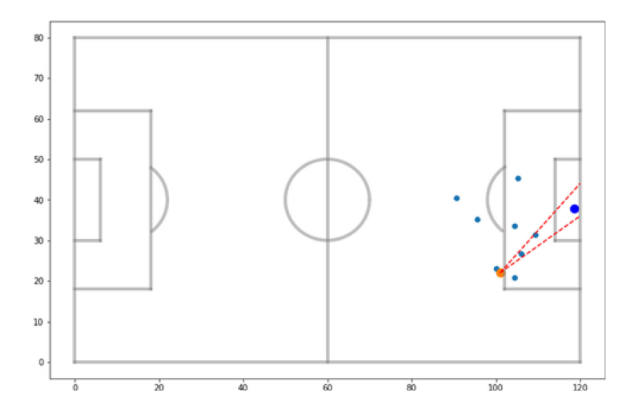
Hewitt and Karakuş (2023)

Methodology

Goal: Infer effect of a specific player on the outcome of a shot

  • Naive approach: Fit GLM (logistic regression) including all players and other features and use classical Wald tests.

    • Problem: High dimensionality (more than 1000 players), sparsity and model misspecification.

  • What about fitting many small models with only one player:

    • Problem: Non-collapsibility(model misspecification).

  • Question: How does Bayesian model averaging perform?

    • How does the high-dimensionality affect the problem?
    • Is non-collapsibility still a problem?

  • Side note: In a current project we use algorithm (i.e. model) agnostic conditional independence tests (COMETs) for this problem.

    • Test the null hypothesis that \(Y\) (shot outcome) is independent of \(X\) (player involved) given \(Z\) (other shot specific features).

A primer on non-collapsibility

Logistic regression setup:

\[Y = I_{\{X + Z + L + \epsilon > 0\}}, \quad \epsilon \sim \text{logistic(0,1)}.\] \(X,Z,\) and \(L\) independent. But all of them influence outcome variable.

  • Consinder fitting two GLMs (both misspecified):

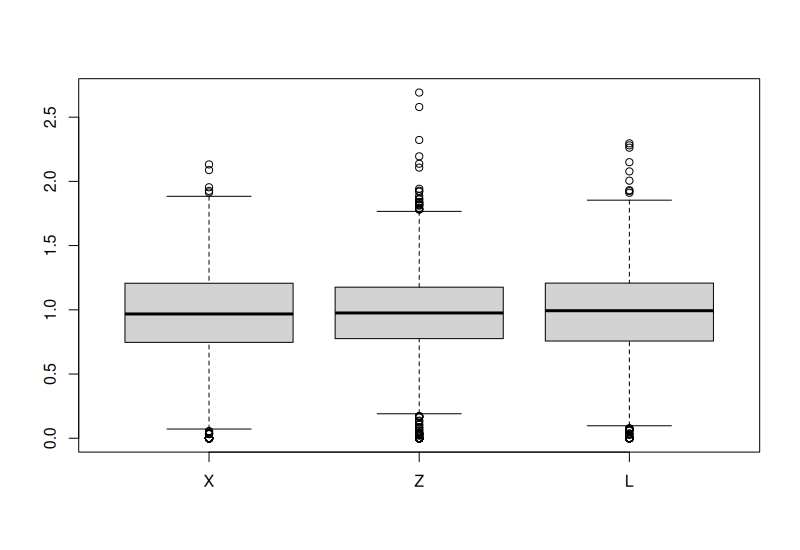
    • \(m_1:\) \[\log(\frac{\pi(X)}{1-\pi(X)}) = \beta_1 X\]

    • \(m_2:\) \[\log(\frac{\pi(X,Z)}{1-\pi(X,Z)}) = \beta_1 X + \beta_2 Z\]

A primer on non-collapsibility

Estimate for \(\beta_1\) in 1000 simulations (\(m_3\) is correct model):

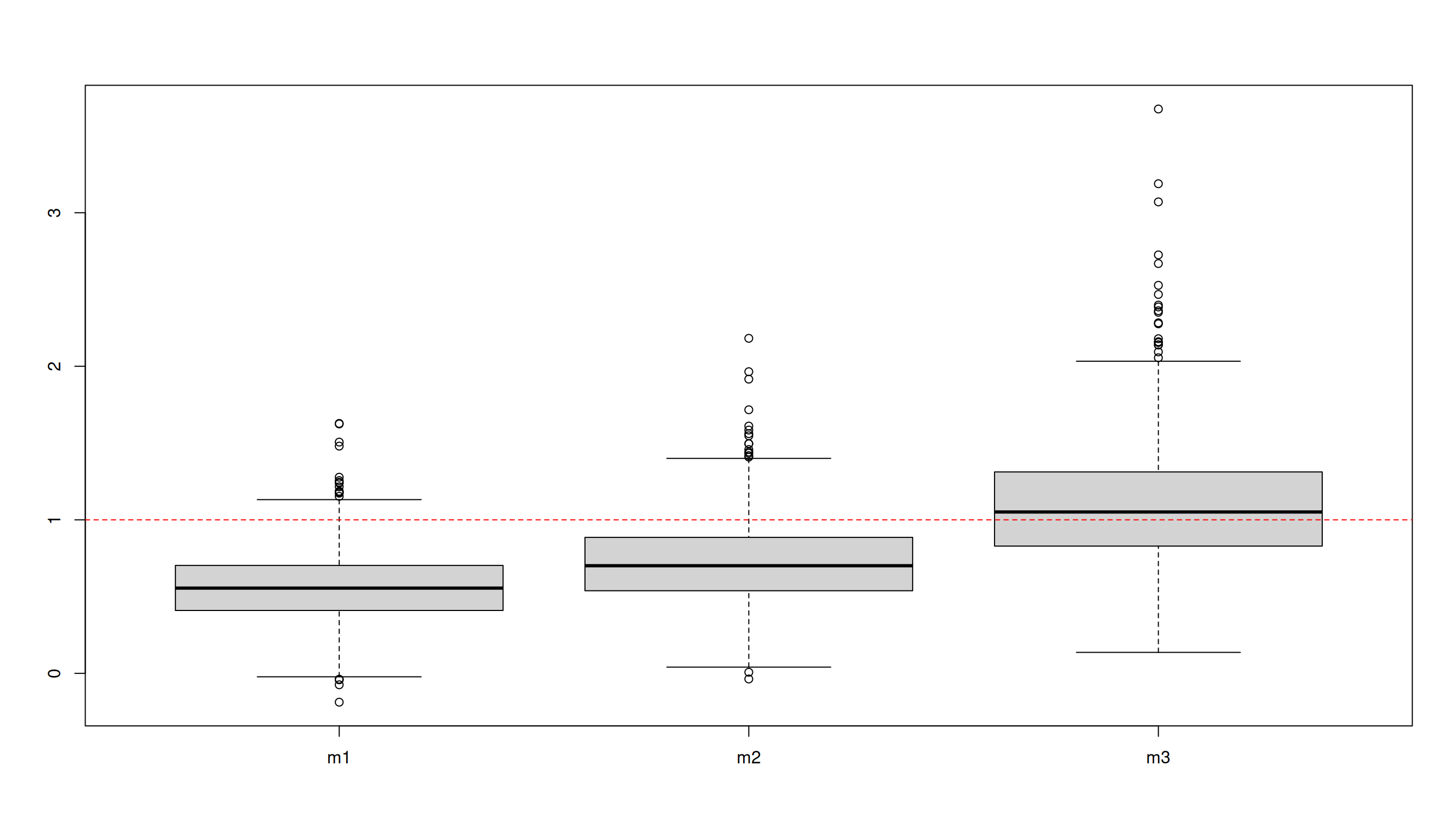
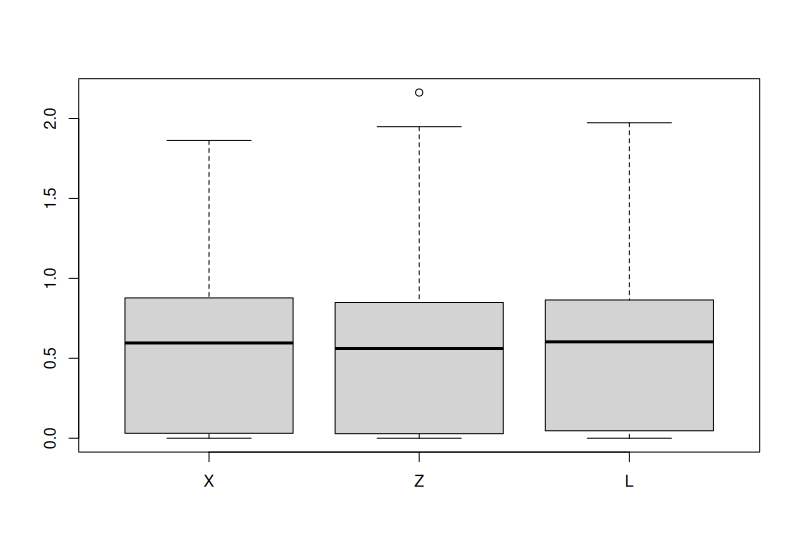
Linear model comparison

As comparison: \(Y = X + Z + L - L_1 + \epsilon, \quad \epsilon \sim \text{N(0,1)}.\)

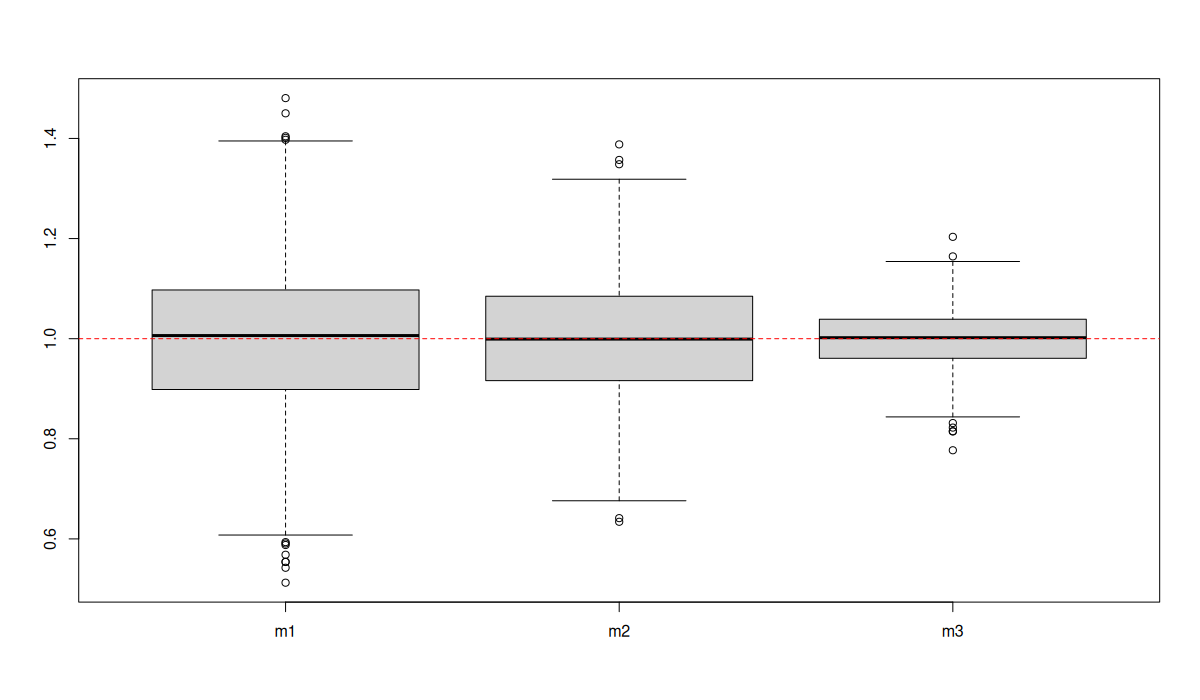
Non-collapsibility in BMA??

Logistic regression setup:

\[Y = I_{\{X + Z + L - L_1 + \epsilon > 0\}}, \quad \epsilon \sim \text{logistic(0,1)}.\] \(X,Z,L,\) and \(L_1\) independent. But all of them influence outcome variable. Furthermore 11 noise (irrelevant) variables in data. Total: 15 regressors (4 of them relevant).

  • Compare two cases:

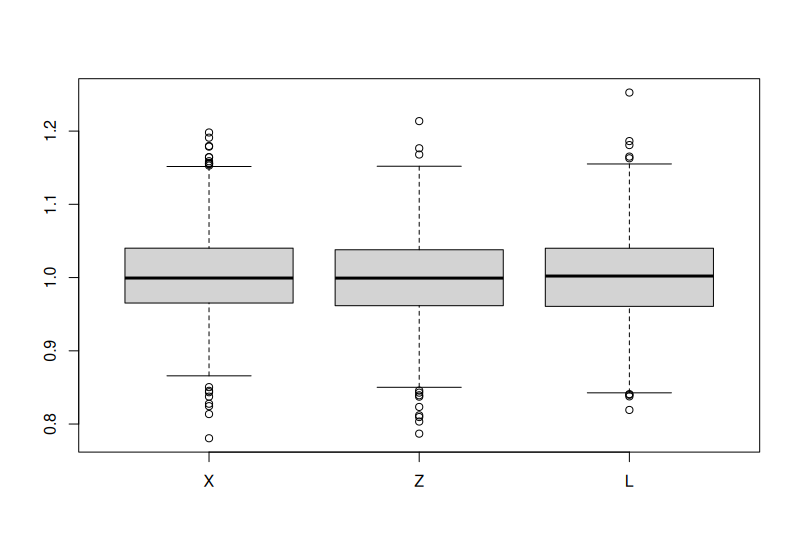
    • BMA with prior inclusion probability of 0.5 for all regressors (a priori models with ~7-8 vars are preferred)

    • BMA with prior inclusion probability of 0.3 (a priori models with 5 vars are preferred)

Non-collapsibility in BMA??

Posterior means from 1000 simulations:

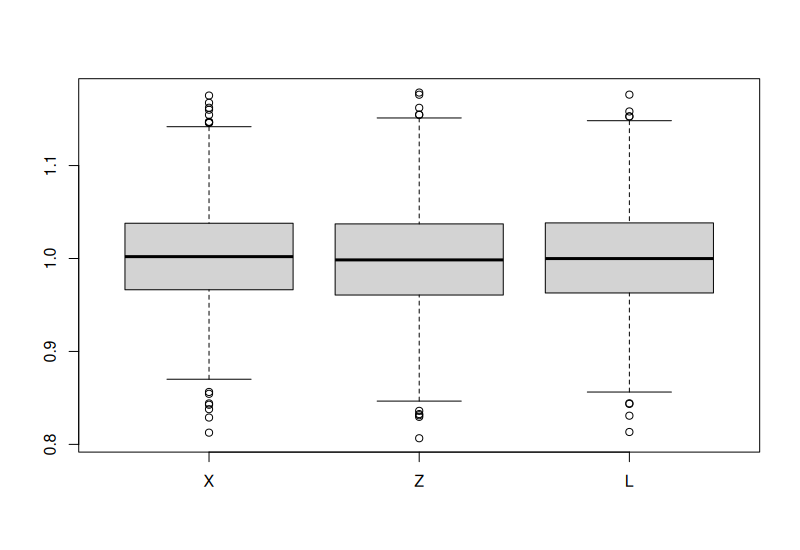
Linear Model BMA

As comparison: \(Y = X + Z + L - L_1 + \epsilon, \quad \epsilon \sim \text{N(0,1)}.\)

References

Hewitt, James H., and Oktay Karakuş. 2023. “A Machine Learning Approach for Player and Position Adjusted Expected Goals in Football (Soccer).” Franklin Open 4: 100034. https://doi.org/https://doi.org/10.1016/j.fraope.2023.100034.